Задание 13
— ЕГЭ — профиль-
Задание № 13. Задачи по стереометрии.
- базовый уровень сложности;
- рекомендуемое время выполнения — 5 минут;
- за верное решение можно получить 1 балл;
- решение не проверяется, на апелляцию не подается;
- все необходимые знания и умения формируются в 10-11 классах.
Информация для учеников. Как работать с материалом, размещенным в этом разделе?
1.Обязательно выполняйте все шаги алгоритма!
2.Обязательно выучить всю теорию. Не тратьте время на попытки решить наугад. Время дорого!
3. Внимательно изучите все образцы решения. Попробуйте самостоятельно воспроизвести эти решения по памяти. «По памяти» — не подглядывая, ни на секунду, ни «одним глазком», ни «чтобы просто убедиться». При решении заданий проговаривайте объяснение полностью.
4. Потренируйтесь в решении дополнительных заданий. Решайте их по алгоритму, отработайте алгоритм так, чтобы выполнять его не задумываясь.
Информация для родителей. Как работать с материалом, размещенным в этом разделе?
Уважаемые неравнодушные и беспокоящиеся родители  !
!
Если Вы хотите проконтролировать уровень своего ребенка или помочь ему в изучении методики решения этого задания, то
-
попросите ученика без каких-либо дополнительных повторений воспроизвести всю теорию. Проверять Вы его можете по тексту на сайте, Вам самим для этого не нужно изучать правила. Воспроизведение должно быть максимально полным и точным.
-
не задавайте наводящих вопросов. Как правило, Ваши вопросы — это скорее подсказки, а они нам не нужны. Пусть ребенок самостоятельно воспроизведет все правила, которые относятся к определенному типу заданий;
-
попросите ученика решить самостоятельно размещенные на сайте образцы. Вы сможете проверить решение по размещенным здесь образцам. Просите ребенка, чтобы он объяснял каждый свой шаг, чтобы избежать механического запоминания образца решения. Ведь этот же самый алгоритм нужно будет повторить в задании с другими числами, размещенными в уравнении по другому, а значит нужно запомнить пошаговую логику, а не перемещение символов.
Дополнение:
Это геометрия, поэтому ВСЕГДА начинайте решение с чертежа, не ленитесь, не делайте никаких выводов о способе решения или ответе, пока не выполните качественный чертеж и не нанесете на него все данные.
Можно ли учить не всю теорию? Нельзя.
Можно ли решать другим способом? Да, конечно. Если Ваш способ никогда Вас не подводит, то ни в коем случае от него не отказывайтесь, не переучивайтесь, у Вас и так все будет хорошо.
Алгоритм
1. Чертеж Вам уже дан (если не дан, то чертите), покажите на нем все, что известно, обозначьте вопрос задачи.
-
- Эту рекомендацию выполняем на бумаге, а не в голове. Аргумент: «Я и так умный, мне не надо» — не оправдывает Ваших периодических (или постоянных) ошибок при выполнении этого задания. А лишь подтверждает необходимость чертить.
2. Перечислите все фигуры, что Вы видите на чертеже. Выберите из них ту, о которой больше всего данных. Используйте эти данные, чтобы найти новые значения. Найдите все, что возможно. Дополните чертеж новыми данными.
-
- Обязательно проанализируйте сначала все данные. Никогда не делайте поспешных выводов. Не пытайтесь сразу после чтения условия выбрать способ решения. Это не страшно, что сразу не понятно, как решать задачу. Просто проанализируйте условие (медленно и полностью). То, что кто-то это делает быстрее и видит все и сразу, не показатель того, что Вы не справляетесь.
3. Подберите фигуру (или элемент фигуры), о которой задан вопрос. Возможно, Вы уже ответили на вопрос задачи, тогда выписывайте ответ.
4. Если на вопрос ответ пока не получен, то кратко (это важно! не произносите лишние слова) сформулируйте, что Вам нужно найти, и что Вам уже известно. Произносите НЕ числа, а названия элементов фигур. Вспомните в каком правиле встречаются такие сочетания элементов. Используйте подходящее правило.
-
- Если выбранная фигура не помогает решить задачу, то подбираем другую фигуру, а не смотрим на чертеж, внушая мозгу, что Вы ничего не понимаете и не знаете. Он послушается Вас и ничего решать не будет!
- Обязательно кратко и четко формулируйте, что Вы видите, и, что Вам нужно найти. «Не лейте воду!» Не подменяйте названия элементов фигур числами, буквами, звуками, фразами «ну, эта штука». Без четкой формулировки мозг не поймет, какие правила он должен вспомнить.
5. Когда удобно или необходимо проводить дополнительные построения
- в равнобедренном треугольнике провести высоту к основанию – получим два равных прямоугольных треугольника.
- в равнобедренной трапеции провести две высоты, получим по бокам два равных прямоугольных треугольника, по центру прямоугольник (или квадрат).
- в окружности провести радиусы так, чтобы получились равнобедренные треугольники.
- в окружности провести радиус к точке касания, чтобы получить прямоугольный треугольник.
6. Иногда полезно заметить, что большую фигуру можно разбить на маленькие равные части.
7. Геометрические задачи также можно решать с помощью уравнений, как и все остальные математические задачи. Смело вводите переменную (или переменные) и составляйте уравнения.
8. Если вспоминать нЕчего, то сначала выучите правила, не мучайте мозг!

Правила
— учим —
-не читаем! не смотрим! учим!-
- Вся эта информация должна быть в памяти. Вы должны воспроизводить ее с любого места в полном объеме без каких-либо дополнительных повторений.
Вы должны самостоятельно видеть, называть, перечислять все фигуры на чертеже (без дополнительных вопросов).
1. Чтобы найти площадь поверхности сложной фигуры, найдите площадь каждой отдельной грани и сложите эти результаты.
2. Чтобы найти объем фигуры с вырезами
- найдите объем воображаемой фигуры без этих вырезов;
- найдите объем вырезанной фигуры;
- вычтите из полного объема объем вырезанной части.
3. Объем параллелепипеда равен произведению его длины, ширины и высоты.
- если одну из сторон параллелепипеда увеличить в n раз, то и объем увеличится в n раз;
- если одну сторону параллелепипеда увеличить в n раз, а вторую в m раз, то объем увеличится в n•m раз.
4. Объем куба равен кубу стороны.
- если сторону куба увеличить (уменьшить) в n раз, то объем куба увеличится (уменьшится) в n³ раз.
5. Объем цилиндра равен произведению площади основания на высоту. Площадь основания цилиндра равна πr².
- если площадь основания цилиндра увеличить (уменьшить) в n раз, то высота жидкости уменьшится (увеличится) в n раз;
- если радиус основания цилиндра увеличить (уменьшить) в n раз, то высота жидкости уменьшится (увеличится) в n² раз.
6. Чтобы найти ВО сколько раз отличается одно значение от другого, нужно большее значение разделить на меньшее.
7. Чтобы найти НА сколько отличается одно значение от другого, нужно из большего значения вычесть меньшее.
8. Если высоты и основания конусов отличаются в n раз, то их объемы отличаются в n³раз.
9. Любую большую фигуру можно разбить на несколько маленьких.
10. Объем шара: V=4πr³/3.
Тренировочные задания
1. Для того чтобы измерить объём детали ее полностью погружают в жидкость, налитую в правильную четырехугольную призму. Найдите объём детали, если уровень жидкости в призме поднялся на 20 см, а сторона основания призмы 30 см. Ответ дайте в кубических сантиметрах.
2. Ящик, имеющий форму куба с ребром 8 см без одной грани, нужно покрасить со всех сторон снаружи. Найдите площадь поверхности, которую необходимо покрасить. Ответ дайте в квадратных сантиметрах.
3. От деревянной правильной шестиугольной призмы отпилили все её вершины (см. рис.). Сколько граней у получившегося многогранника?
4. Сколько литров воды помещается в куб со стороной 20 см? В одном литре 1000 кубических сантиметров.
5. Во сколько раз объем одной из коробок, имеющих форму правильной четырёхугольной призмы, больше, если первая коробка в три ниже второй, а вторая вдвое шире первой?
6. Даны две правильные четырёхугольные пирамиды. Объём второй пирамиды равен 8. У второй пирамиды высота в 2 раза больше, а сторона основания в 3 раза меньше, чем у первой. Найдите объём первой пирамиды.
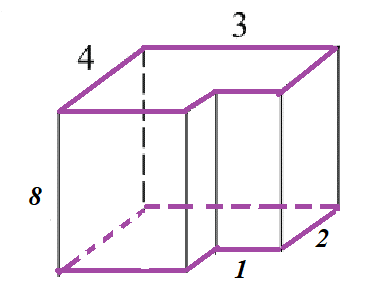
7. Найдите площадь поверхности многогранника и его объем, изображенного на рисунке (все двугранные углы прямые).
8. В цилиндрический сосуд налили 1000 см³ воды. Уровень воды при этом достигает высоты 25 см. В жидкость полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 12 см. Чему равен объем детали? Ответ выразите в см³.
9. В цилиндрическом сосуде уровень жидкости 24 см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй сосуд, диаметр которого в 3 раза меньше первого? Ответ выразите в см.
10. Даны две кружки цилиндрической формы. Первая кружка в полтора раза ниже второй, а вторая вдвое шире первой. Во сколько раз объём второй кружки больше объёма первой?
11. Шар радиусом 3 см имеет массу 162 грамма. Чему равна масса шара, изготовленного из того же материала, с радиусом 9 см? Ответ дайте в граммах.
12. В сосуде, имеющем форму конуса, уровень жидкости достигает треть высоты. Объём сосуда 540 мл. Чему равен объём налитой жидкости? Сколько жидкости еще нужно долить в сосуд, чтобы он заполнен полностью? Ответ дайте в миллилитрах.