ЕГЭ-математика-база-задание 14
— действия с целыми и дробными числами —
- базовый уровень сложности;
- рекомендуемое время выполнения- 5 минут;
- за верное решение можно получить 1 балл;
- решение не проверяется, на апелляцию не подается;
- необходимые знания и умения формируются в 1-5 классах;
Информация для учеников. Как работать с материалом, размещенным в этом разделе?
1шаг. Обязательно выучить всю теорию. Не тратьте время на попытки решить наугад. Время дорого!
2 шаг. Внимательно изучите все образцы решения. Попробуйте самостоятельно воспроизвести эти решения по памяти. «По памяти» — не подглядывая, ни на секунду, ни «одним глазком», ни «чтобы просто убедиться». При решении заданий проговаривайте объяснение полностью.
3 шаг. Потренируйтесь в решении дополнительных заданий. Решайте их по алгоритму, отработайте алгоритм так, чтобы выполнять его не задумываясь.
Информация для родителей. Как работать с материалом, размещенным в этом разделе?
Уважаемые неравнодушные и беспокоящиеся родители  !
!
Если Вы хотите проконтролировать уровень своего ребенка или помочь ему в изучении методики решения этого задания, то
-
попросите ученика без каких-либо дополнительных повторений воспроизвести всю теорию. Проверять Вы его можете по тексту на сайте, Вам самим для этого не нужно изучать правила. Воспроизведение должно быть максимально полным и точным.
-
не задавайте наводящих вопросов. Как правило, Ваши вопросы — это скорее подсказки, а они нам не нужны. Пусть ребенок самостоятельно воспроизведет все правила, которые относятся к определенному типу заданий;
-
попросите ученика решить самостоятельно размещенные на сайте образцы. Вы сможете проверить решение по размещенным здесь образцам. Просите ребенка, чтобы он объяснял каждый свой шаг, чтобы избежать механического запоминания образца решения. Ведь этот же самый алгоритм нужно будет повторить в задании с другими числами, размещенными в уравнении по другому, а значит нужно запомнить пошаговую логику, а не перемещение символов.
Дополнение:
Можно ли учить не всю теорию? Нельзя.
Чем больше уравнений Вы прорешаете, тем быстрее правила закрепятся в памяти, поэтому практика, практика и еще раз практика.
Можно ли решать другим способом? Да, конечно. Если Ваш способ никогда Вас не подводит, то ни в коем случае от него не отказывайтесь, не переучивайтесь, у Вас и так все будет хорошо.
Важная рекомендация
для тех, кто так и не научился складывать и вычитать в пределах 10, не смог выучить таблицу умножения:
— срочно сказать: «Спасибо!» всем, кто говорил Вам: «Не можешь запомнить и не надо. Я вот никогда не знал, и сейчас не знаю, просто спокойно считаю на калькуляторе!»
— выйти с пикетом на Красную площадь: «Даешь калькулятор на ЕГЭ по математике!»
— вымойте руки и приготовьтесь использовать на ЕГЭ пальцы, их разрешают брать с собой, и они реально могут Вам помочь (это не сарказм);
— ну и для тех, кто еще способен убить в себе Обломова, скачиваем таблицу умножения, таблицу сложения и вычитания в пределах 10 и УЧИМ.

Правила
1. С чего начать решение любого примера? Если математика не самый лучший друг, то расставляем порядок действий. Как расставить порядок действий:
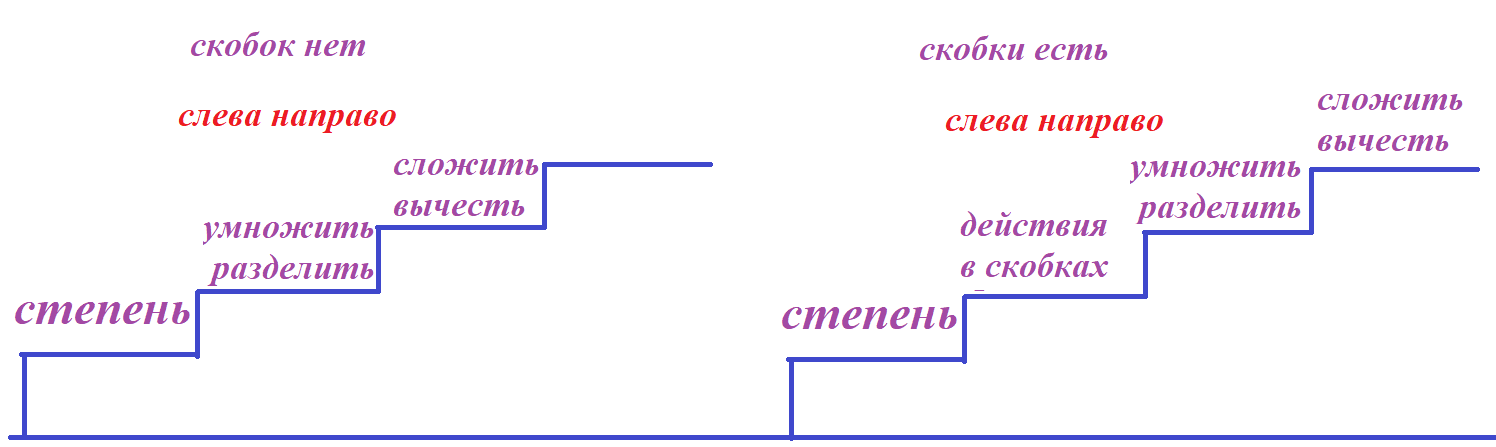
- если скобок нет, то
- 1 шаг: возводим в степень;
- 2 шаг: слева направо по порядку умножаем и делим;
- 3 шаг: слева направо по порядку (после умножения и деления) складываем и вычитаем.
- если есть скобки, то
- 1 шаг: возводим в степень в скобках;
- 2 шаг: умножаем и делим в скобках;
- 3 шаг: складываем и вычитаем в скобках;
- 4 шаг: возводим в степень за скобками;
- 5 шаг: слева направо по порядку умножаем и делим (за скобками);
- 6 шаг: слева направо по порядку складываем и вычитаем (за скобками).
- существуют ли правила, которые позволяют менять такой порядок действий? Да, но работают они не всегда, поэтому пользуйтесь универсальным порядком.
3. Дробь с дробной чертой — обыкновенная дробь.
4. Дробь с запятой — десятичная дробь.
5. Не всякую обыкновенную дробь можно представить в виде десятичной, поэтому не надо стараться каждую обыкновенную дробь превращать в десятичную.
6. Дробная черта означает действие «деление». Не все числа делятся друг на друга, поэтому не надо стараться все числа поделить друг на друга.
7. Если число не делится нацело на другое число, не надо отбрасывать бесконечный «хвост». Запишите это деление в виде дроби и работайте дальше с обыкновенными дробями.
8. В задании 1 нельзя округлять! Если не получается дать ответ в виде целого числа или конечной десятичной дроби, пересчитывайте! У Вас ошибка в вычислениях.
9. Если нужно умножить обыкновенную дробь на десятичную, нужно десятичную дробь представить в виде обыкновенной, а затем выполнить умножение обыкновенных дробей. Можно ли для умножения обыкновенную дробь превратить в десятичную? Да, можно, но не всегда, поэтому пользуйтесь лучше способом, который работает всегда.
10. Если нужно перемножить обыкновенные дроби, нужно
- перемножить числители друг на друга;
- перемножить знаменатели друг на друга;
- если есть возможность, то сокращать.
11. Чтобы превратить обыкновенную дробь в десятичную, необходимо числитель поделить на знаменатель.
12. Числитель — это аналог делимого, знаменатель — аналог делителя.
13. Ответы на ЕГЭ даются только в виде целых чисел или конечных десятичных дробей, не забудьте об этом.
14. Чтобы перемножить десятичные дроби, нужно записать дроби в столбик так, чтобы
- первой была записана более длинная дробь (не обязательно бОльшая, а длинная);
- вторую дробь записать так, чтобы последние цифры первой и второй дроби оказались друг под другом (не запятые! а последние цифры);
- перемножить дроби, не обращая внимания на запятые;
- посчитать количество цифр справа от запятой у первого и второго числа (вместе);
- отсчитать в результате справа столько же цифр, сколько получилось в предыдущем пункте, и поставить запятую;
- если цифр в результате не хватит, то дописать СЛЕВА нули.
15. Чтобы разделить обыкновенные дроби друг на друга, нужно
- переписать первую дробь без изменений;
- заменить деление на умножение;
- вторую дробь перевернуть;
- умножить числители друг на друга;
- умножить знаменатели друг на друга;
- если есть возможность, то сократить;
- сокращать можно только множители.
16. Чтобы сложить (вычесть) десятичные дроби, нужно
- записать дроби друг под другом так, чтобы запятая оказалась под запятой;
- если справа от запятых дроби окажутся разной длины, то более короткой дроби дописать в конце нули;
- выполнить сложение (вычитание) дробей, как целых чисел;
- в ответе поставить запятую ПОД предыдущими запятыми.
17. Вычитать можно только из бОльшего модуля меньший. Наоборот нельзя, никогда!.
Тренировочные задания
1. Действия с обыкновенными дробями: перейти к тренировке