1. Треугольник — многоугольник, состоящий из трех отрезков, соединяющих три точки, не лежащие на одной прямой.
2. У каждого треугольника: три угла, три вершины, три стороны.
3. Сумма внутренних углов любого треугольника равна 180º.
4. Внешний угол треугольника — угол смежный с внутренним углом треугольника.
5. Равносторонний треугольник — правильный многоугольник, у которого все три стороны и три угла равны. Каждый угол равностороннего треугольника равен 60º.
6. Равнобедренный треугольник — треугольник, у которого две стороны равны, они называются боковыми, третья сторона называется основанием.
7. Теорема: углы при основании равнобедренного треугольника равны.
8. Углы при основании равнобедренного треугольника не могут быть тупыми.
9. Теорема: биссектриса равнобедренного треугольника, проведенная к основанию треугольника, является также медианой и высотой.
10. Прямоугольный треугольник — треугольник, у которого один угол равен 90º. Два остальных угла острые, их сумма 90º.
11. Прямоугольный треугольник может быть равнобедренными, тогда его углы равны 90º, 45º, 45º.
12. Остроугольный треугольник — треугольник, у которого все углы острые.
13. Тупоугольный треугольник — треугольник, у которого один угол тупой.
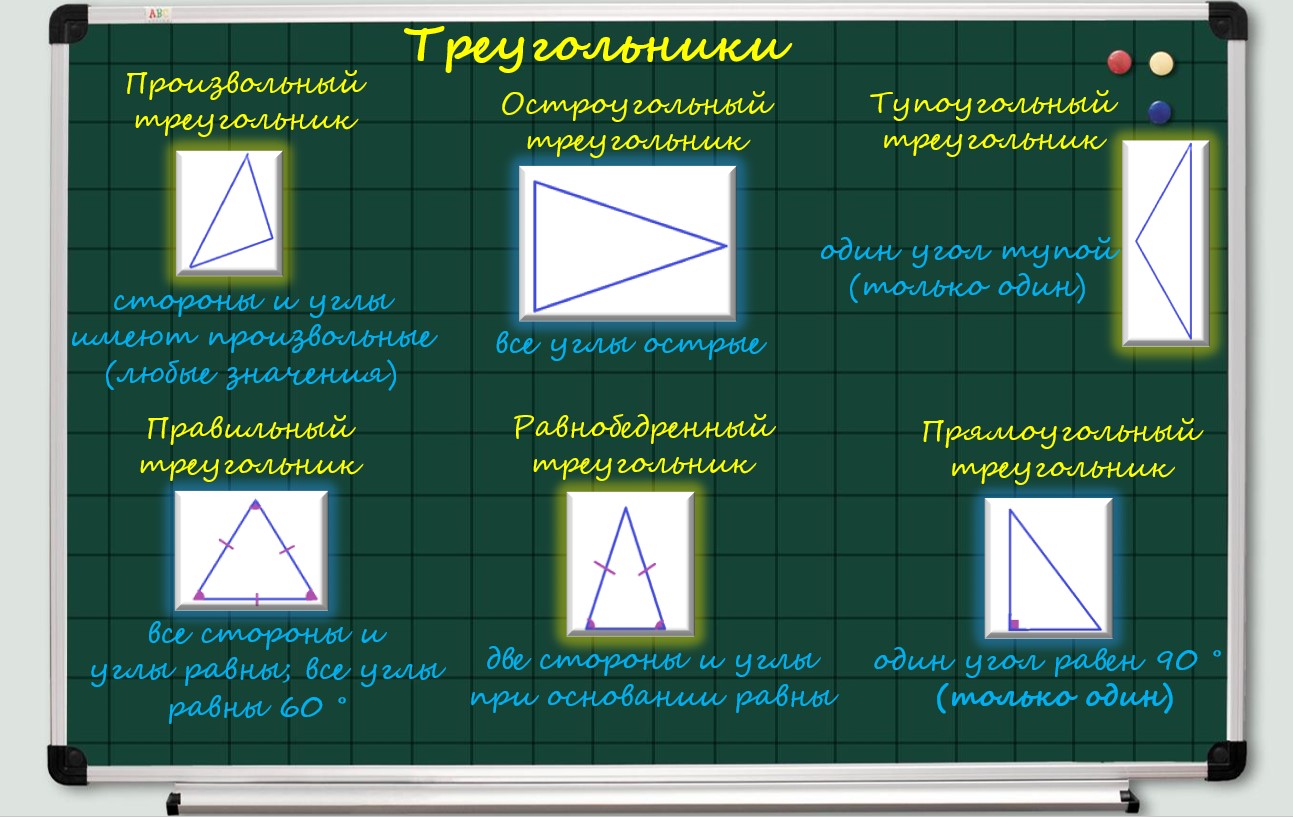
14. В треугольнике напротив бОльшего угла лежит бОльшая сторона.
15. Неравенство треугольников: сумма любых двух сторон треугольника должна быть больше третьей стороны.
16. Медиана — отрезок, проведенный из вершины угла к середине противолежащей стороны. У каждого треугольника три медианы, все они лежат внутри треугольника.
17. Биссектриса — луч, который проведен из вершины треугольника и делящий этот угол пополам.
18. Высота — перпендикуляр, проведенный из вершины треугольника к противолежащей стороне. У каждого треугольника 3 высоты. У прямоугольного треугольника две стороны совпадают с катетами.
19. Не все высоты треугольника могут лежать внутри треугольника. Если в треугольнике есть тупой угол, то высоты, проведенные из острых углов , будут опираться на продолжение сторон треугольника.
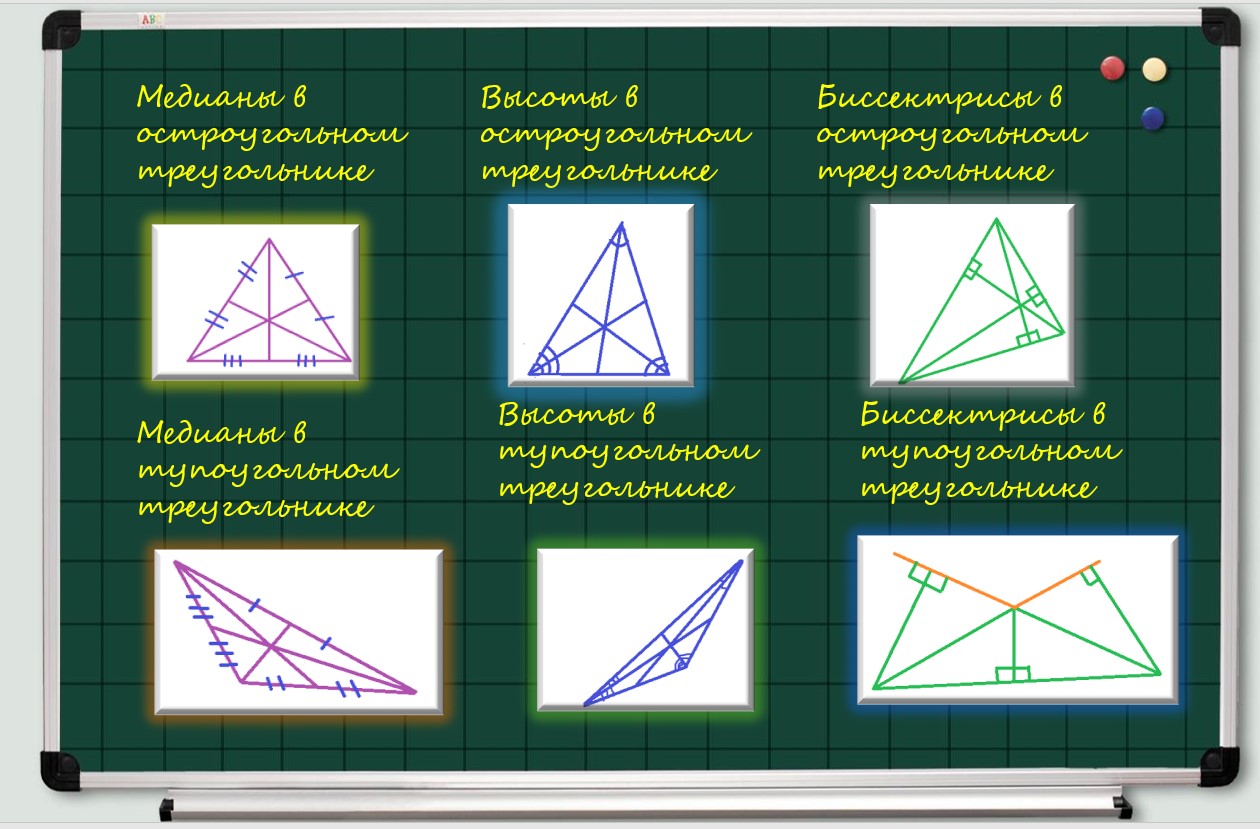
20. В прямоугольном треугольнике стороны имеют особые названия:
- катеты (две меньшие стороны);
- гипотенуза (самая большая сторона, лежит напротив угла 90º).
21. Катет, лежащий напротив угла 30º равен половине гипотенузы.
22. Если катет равен половине гипотенузы, то напротив него лежит угол 30º.
23. Треугольники называются равными, если элементы одного треугольника (стороны и углы) соответственно равны углам другого треугольника. Равные треугольники при наложении совпадают. Площади и периметры равных треугольников равны.
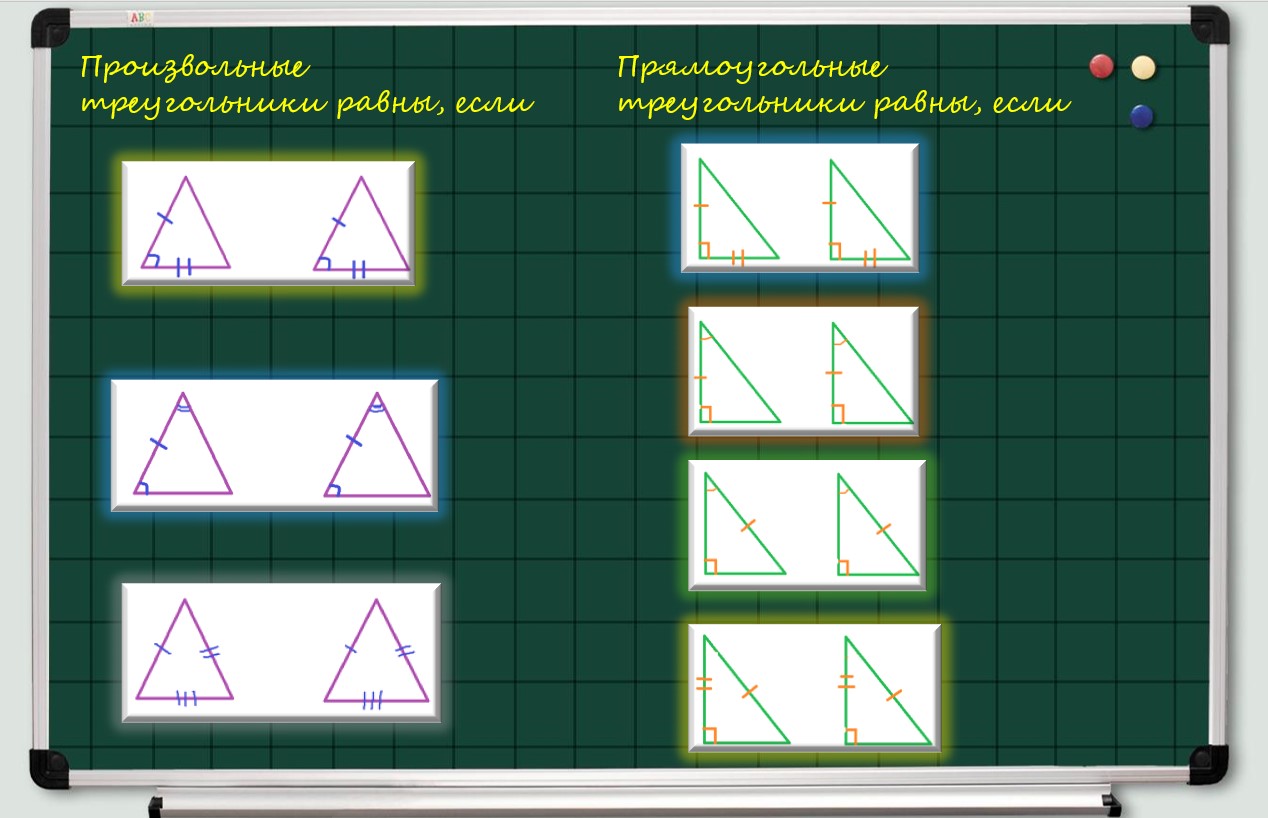
24. Признаки равенства треугольников:
- первый признак (теорема): если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны;
- второй признак (теорема): если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим углам другого треугольника, то такие треугольники равны;
- третий признак (теорема): если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
25. Признаки равенства прямоугольных треугольников:
- если катеты одного прямоугольного треугольника соответственно равны катетам другого прямоугольного треугольника, то такие треугольники равны;
- если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого прямоугольного треугольника, то такие треугольники равны;
- теорема: если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны;
- теорема: если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны.
26. Периметр любого треугольника — сумма длин всех (трех) сторон.
27. Площадь:
- любого треугольника:
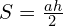, h — высота треугольника, a — сторона, к которой проведена высота; - прямоугольного треугольника:
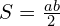, a,b — катеты прямоугольного треугольника.
28. Квадрат — четырехугольник, у которого все стороны равны друг другу, а все углы равны 90º.
29. Прямоугольник — четырехугольник, у которого противолежащие стороны равны, а все углы равны 90º.
30. Фигуры на плоскости называются многоугольниками, а фигуры в пространстве называются многогранниками.
31. Любая фигуры на плоскости состоит из сторон и вершин.
32. Любая фигура в пространстве состоит из ребер, граней, вершин.
33. Прямоугольный параллелепипед — это многогранник, гранями которого являются прямоугольники, все углы равны 90º.
34. Куб — параллелепипед, у которого все ребра равны, а все углы равны 90º.
35. Периметр любой фигуры — сумма длин всех сторон (ребер).
36. Площадь:
- любого треугольника: S=ab:2, a, b — стороны треугольника;
- прямоугольного треугольника: достраиваем треугольник до прямоугольника, находим его площадь и делим ее пополам;
- площадь поверхности параллелепипеда и куба равна сумме площадей каждой грани.
37. Объем параллелепипеда: V=abc, a — длина, b — ширина, c — высота параллелепипеда.
38. Объем куба: V=a³, a — сторона куба.