1. Фигуры на плоскости называются многоугольниками, а фигуры в пространстве называются многогранниками.
2. Стереометрия — раздел геометрии, который изучает фигуры в пространстве.
3. Любая фигура в пространстве состоит из ребер, граней, вершин.
4. Многогранники бывают выпуклые и невыпуклые. У выпуклых многогранников вся фигура лежит с одной стороны от плоскости каждой грани.
5. Призма — многогранник состоящий из двух одинаковых параллельных многоугольников (оснований) и соединяющих их боковых граней.
6. Если боковые грани призмы перпендикулярны ее основаниям, то такую призму называют прямой.
7. Прямая призма, основаниями которой являются правильные многоугольники называется правильной. Боковые грани — не обязательно правильные многоугольники.
8. Прямоугольный параллелепипед — это прямая призма, гранями которой являются прямоугольники.
9. Куб — параллелепипед, у которого все ребра равны, а все углы равны 90º. Куб — это правильная призма..
10. Параллелепипед — четырехугольная призма, основаниями которой являются параллелограммы. Все 6 граней параллелепипеда — параллелограммы.
11. Четыре диагонали параллелепипеда пересекаются, и точкой пересечения делятся пополам.
12. Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений (длины, ширины, высоты).
13. Если две прямые в пространстве параллельны третьей, то они параллельны.
14. Основаниями призмы могут быть не только прямоугольники и квадраты, но и треугольники (треугольная призма), шестиугольники (шестиугольная призма) и т.д.
15. Если боковые грани не перпендикулярны основаниям, то призма называется наклонной.
16. Пирамида называется правильной, если ее основание правильный многоугольник. Высота правильной пирамиды опускается из вершины в центр основания.
17. Тетраэдр — треугольная пирамида, в основании лежит треугольник.
18. Перпендикуляр, проведенный от одного основания к другому, называется высотой призмы (цилиндра).
19. Перпендикуляр, проведенный от вершины пирамиды (конуса) к основанию, называется высотой пирамиды (конуса).
20. Высота боковой грани правильной пирамиды, проведенная из вершины, называется апофемой.
21. Цилиндр — фигура вращения, получающаяся при вращении прямоугольника вокруг одной из своих сторон. Получающиеся круги называются основаниями, они параллельны друг другу, их радиус — радиусом цилиндра.
22. Отрезок, проходящий по боковой стороне цилиндра перпендикулярно основаниям, называется образующей. Все образующие цилиндра равны друг другу, провести их можно бесконечно много.
23. Линия, проходящая через центры оснований цилиндра, называется осью цилиндра.
24. Конус — фигура вращения, получающаяся при вращении прямоугольного треугольника, вокруг одного из своих катетов. Поверхность, образующаяся при движении его гипотенузы, является боковой поверхностью конуса. Сама гипотенуза является образующей конуса. Все образующие конуса равны друг другу, провести их можно бесконечно много. Катет, вокруг которого происходило вращение, является осью конуса и его высотой. Фигура вращения второго катета — это круг, который является основанием конуса.
25. Объем параллелепипеда:
- V=abc, a — длина, b — ширина, c — высота параллелепипеда;
- V=a³, a — сторона куба;
- V=Sh, S — площадь основания (любого), h — высота.
26. Объем пирамиды (и конуса): V=Sh/3; S — площадь основания, h — высота пирамиды (конуса).
27. Площадь боковой поверхности цилиндра: S=2πrh.
28. Площадь боковой поверхности конуса:
- S=
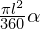, l — длина образующей; - S=πrl, r — радиус основания конуса, l — длина образующей.
29. Площадь полной поверхности цилиндра: S=2πrh+2πr², r — радиус основания (любого), h — высота цилиндра.
30. Площадь полной поверхности конуса: S=πrl+πr², r — радиус основания, l — длина образующей.
31. Сферой называется поверхность, состоящая из всех точек, равноудаленных от общего центра. Расстояние от центра до любой такой точки называется радиусом. Диаметр — отрезок соединяющий две точки сферы, проходящий через ее центр.
32. Сфера — фигура вращения, получающаяся при вращении полуокружности вокруг своего диаметра.
33. Шар — тело, ограниченное сферой. Центр, радиус и диаметр сферы также называются центром, радиусом, диаметром шара.
34. Шар — фигура вращения, получающаяся при вращении полукруга вокруг своего диаметра.
35. Объем шара: V=
.
36. Площадь сферы (или площадь поверхности шара): S=4πr².
37. Равные тела имеют равные объемы.
38. Если тело составлено из нескольких тел, то его объем равен сумме объемов отдельных тел.