ОГЭ-математика-задание 11

Задание 11

Графики и функции

базовый уровень сложности;
рекомендуемое время выполнения- 5 минут;
за верное решение можно получить 1 балл;
решение не проверяется, на апелляцию не подается;
необходимые знания и умения формируются в 6-9 классах.

Общие правила

Общие правила

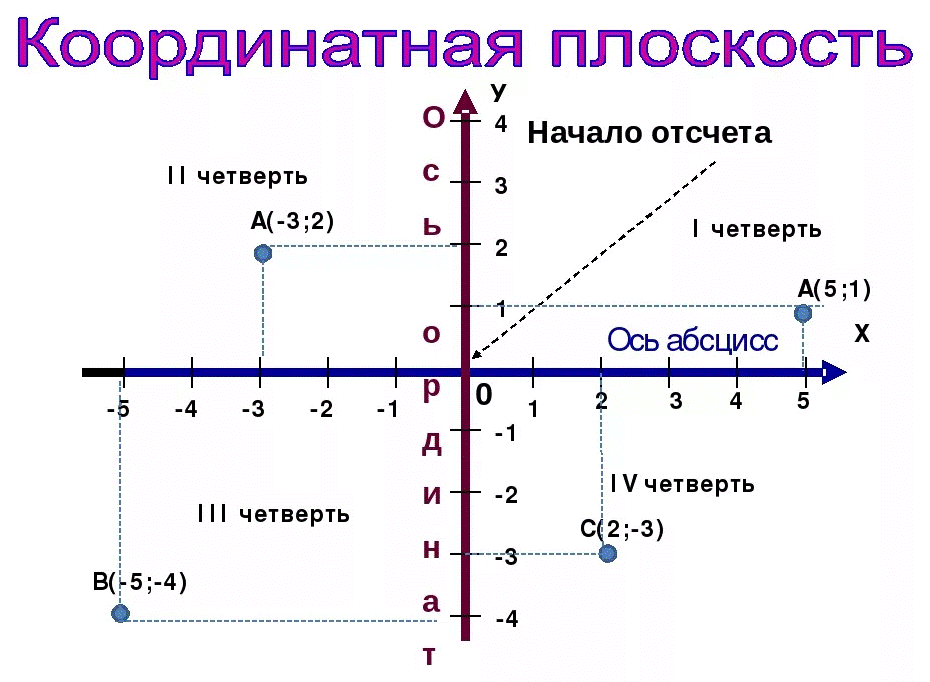
1. Каждая точка графика имеет две координаты: х и у.

2. Графики строятся на координатной плоскости.

3. Координатная плоскость состоит из

горизонтальной оси ОХ, направленной направо;
вертикальной оси ОУ направленной вверх;
единичного отрезка для каждой оси (у каждой оси может быть свой единичный отрезок);

4. При построении графика мы выбираем любые удобные для нас значения координаты х, поэтому х называется независимой переменной;

5. При построении графика координату у мы рассчитываем по заданной формуле, подставляя в нее произвольный х, координата у называется зависимой переменной;

6. Оси разбивают координатную плоскость на 4 четверти, которые нумеруются, начиная с правой верхней, против часовой стрелки.

[свернуть]

Виды графиков и функций

Виды графиков и функций

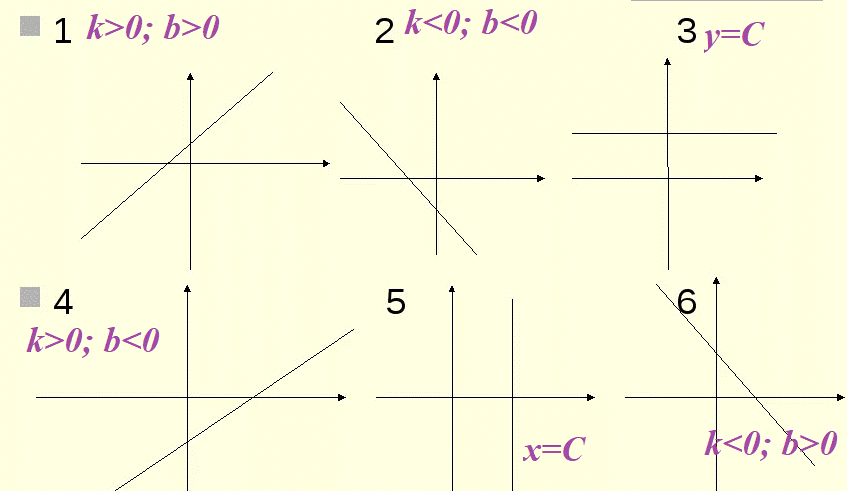
1. Линейная функция

стандартный вид: y=kx+b
- если к > 0, то прямая возрастает (слева направо) (идем по горке вверх);
- если к < 0, то прямая убывает (слева направо) (скатываемся с горки вниз);
- если b > 0, то прямая пересекает ось ОУ выше оси ОХ;
- если b < 0, то прямая пересекает ось ОУ ниже оси ОХ;
графиком является прямая линия
- для построения графика нужны две точки;
частные случаи линейных функций и их графиков:
- у=х — прямая проходит через точку пересечения осей;
- у=с (с — любое число) — прямая проходит через число С строго горизонтально (как горизонт);
- х=с (с — любое число) — прямая проходит через число С строго вертикально (как столб).

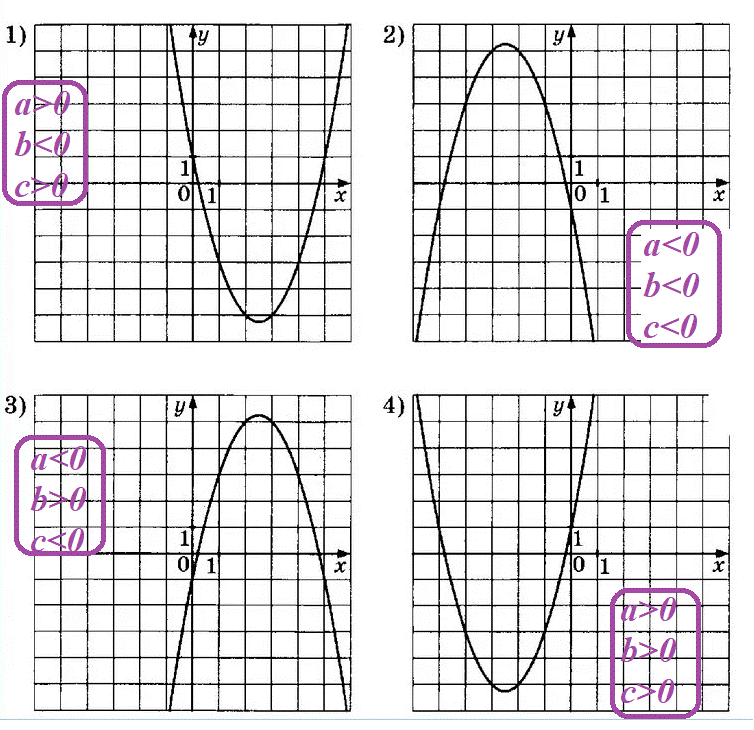
2. Квадратичная функция

стандартный вид: y= ax²+bx+c
- если а > 0
  - ветви параболы смотрят вверх (парабола улыбается);
  - b > 0, то вершина параболы смещена влево от 0;
  - b < 0, то вершина параболы смещена вправо от 0;
  - c > 0, то парабола пересекает ось ОУ выше 0;
  - c < 0, то парабола пересекает ось ОУ ниже 0;
- если a < 0
  - ветви параболы смотрят вниз;
  - b > 0, то вершина параболы смещена вправо от 0;
  - b < 0, то вершина параболы смещена влево от 0;
  - c > 0, то парабола пересекает ось ОУ выше 0;
  - c < 0, то парабола пересекает ось ОУ ниже 0;
графиком является парабола
- для построения графика нужны минимум 5 точек;

3. Обратная пропорциональность

стандартный вид:
$y=\frac{k}{x}$
- если к > 0, то ветви графика расположены в 1 и 3 четвертях;
- если к < 0, то ветви графика расположены во 2 и 4 четвертях;
графиком является гипербола
- для построения графика нужны минимум 6 точек;

[свернуть]

Алгоритм решения

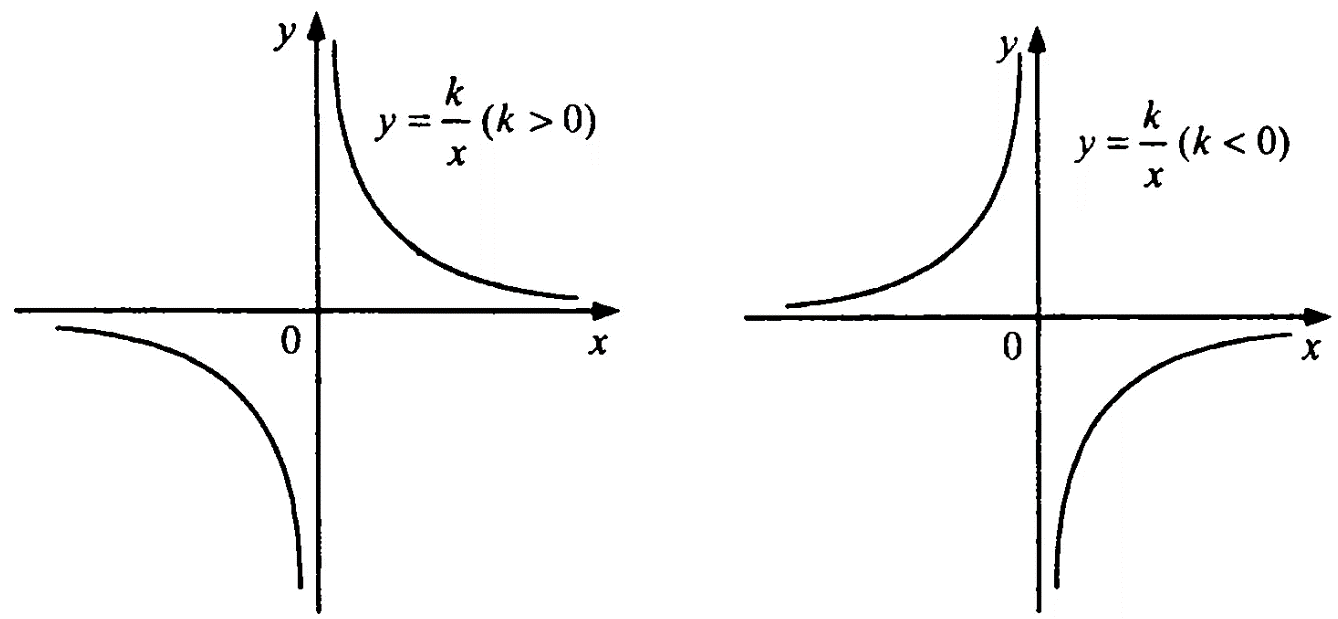
Алгоритм решений

1. Определите для каждого графика его тип.

2. Определите и подпишите для каждого графика знаки каждого коэффициента из стандартного вида.

3. Определите для каждой формулы тип функции.

4. Определите и подпишите для каждой формулы знаки коэффициентов из стандартного вида.

5. Найдите совпадения между подписями к графикам и функциям.

[свернуть]

Образцы решения

Образцы решения

[свернуть]

Тренировочные задания

Тренировочные задания

[свернуть]