Определение подобия треугольников

Два треугольника называются подобными, если углы первого треугольника равны углам второго треугольника или, если соответствующие стороны одного треугольника пропорциональны сторонам второго треугольника.

Что значит «пропорциональны»?

стороны одного треугольника пропорциональны сторонам другого треугольника, если
$\frac{a}{m}=\frac{b}{n}=\frac{c}{k}=k$
- k- коэффициент подобия (или коэффициент пропорциональности).

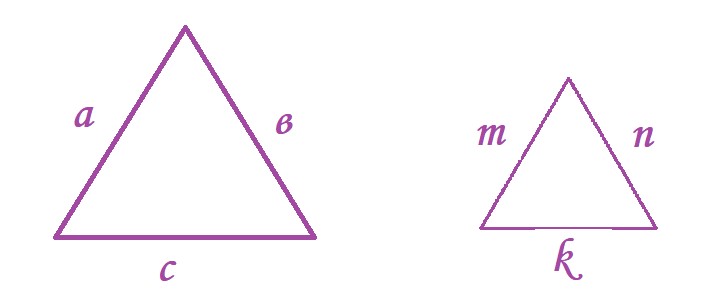
Какие стороны являются соответствующими?

если подобные треугольники наложить друг на друга равными углами (должны совпасть все три угла), то совпавшие стороны и будут соответствующими.

Примечание:

равными фигурами называются фигуры одинаковой формы и одинакового размера;
подобными фигурами называются фигуры одинаковой формы, но разного размера;
термин «соответствующие» равнозначен термину «соответственные».

При решении задач, чтобы доказать, что треугольники подобны, ищем пары равных углов и пары пропорциональных сторон.

Задачи для тренировки

1. Являются ли равными любые два подобных треугольника? Подобны ли любые два равных треугольника? Назовите соответствующий коэффициент подобия.
2. Могут ли быть подобными прямоугольный и тупоугольный треугольники?
3. Два треугольника подобны с коэффициентом 0,25. Во сколько раз стороны одного треугольника больше соответствующих сторон другого?

4. На рисунках ΔABC ∼ ΔMKN. По данным рисунка найдите x и y.

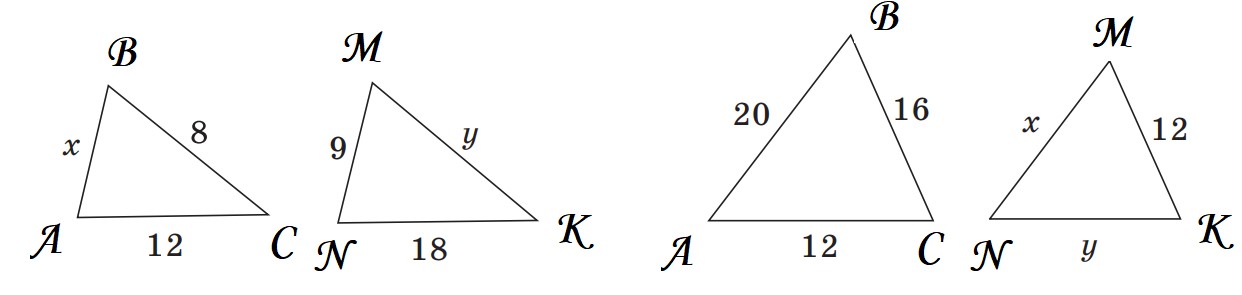
5. Прямая KM параллельна стороне AC треугольника ABC. Найдите отрезок MC, если: а) AK = 2 см, KB = 6 см, BM = 9 см; б) AK:KB = 2:3, BC = 10 см.

6. Прямая KM параллельна стороне AC треугольника ABC. Найдите отрезок AB, если AK = 6 см, BM:MC= 4:3.
7. Известно, что ΔABC∼ΔDEF . Найдите: а) угол C, если ∠А= 45°, ∠Е =110°; б) угол F, если ∠ В=80°, ∠А = ∠C.
8. Найдите острые углы прямоугольного треугольника, если в подобном ему треугольнике разность наибольшего и наименьшего углов равна 70°.

9. Докажите по определению, что любые два равносторонних треугольника подобны.
10. Докажите от противного, что тупоугольный и равносторонний треугольники не могут быть подобными.

11. Известно, что ΔABC∼ΔDEF, причем ∠D=70°, ∠B=55°. Докажите, что AB=AC.
12. Известно, что ΔABC ∼ΔKMN, причем ∠A+ ∠M=90°. Докажите, что AB — наибольшая сторона треугольника ABC.
13. Докажите, что треугольник с вершинами в серединах сторон данного треугольника подобен данному. Чему равен коэффициент подобия?
14. В треугольнике ABC точки D и E — середины сторон AB и ABC соответственно. Докажите, что ΔABC ∼ΔDBE, и найдите коэффициент подобия.

15. Каждый из двух неравных, но подобных треугольников имеет стороны длиной 12 см и 18 см. Найдите неизвестные стороны этих треугольников.
16. Треугольники со сторонами a, b, c и b, c, d подобны. Докажите, что коэффициент подобия не может быть равным 2.

17. Диагональ AC делит трапецию ABCD (AD||BC) на два подобных треугольника ABC и ACD. Найдите AC, если BC = 4 см, AD = 9 см.
18. Диагональ AC трапеции ABCD (AD||BC) равна стороне CD и делит трапецию на два подобных треугольника ABC и ACD. Найдите периметр трапеции, если AB = 9 см, CD = 12 см.

19. Докажите, что треугольник, вершинами которого являются середины сторон данного треугольника, подобен данному треугольнику.

20. Стороны АВ, ВС, АС треугольника АВС пропорциональны сторонам DE, EF, FD треугольника DEF, угол С=50°, угол D= 70°. Найдите остальные углы треугольников.

21. На стороне ВС треугольника АВС отмечена точка М так, что ΔАВМ∼ΔАВС. Найдите АВ, если ВМ=4, СМ=5.

22. .

[свернуть]